Let’s say we have a piece of code ![]() which can be executed using states
which can be executed using states ![]() as inputs. And let’s say this execution is described by a big-step semantics
as inputs. And let’s say this execution is described by a big-step semantics ![]() , which is a binary relation on states in
, which is a binary relation on states in ![]() . That is,
. That is, ![]() means
means ![]() can produce output
can produce output ![]() on input
on input ![]() .
.
There are two approaches to reasoning about the behavior of ![]() . The first one is to defend it: prove that only correct executions exist. Failing to prove correctness is not the same as proving incorrectness. The second approach is to attack it: try to find incorrect executions to exploit or remove. Failing to prove incorrectness is not the same as proving correctness.
. The first one is to defend it: prove that only correct executions exist. Failing to prove correctness is not the same as proving incorrectness. The second approach is to attack it: try to find incorrect executions to exploit or remove. Failing to prove incorrectness is not the same as proving correctness.
Forward Correctness Reasoning
In forward reasoning, we are given a precondition ![]() , which ranges over subsets
, which ranges over subsets ![]() of states, and we look for the reachable set of outputs
of states, and we look for the reachable set of outputs
(1) ![]()
that it can produce. This is also known as the strongest postcondition, but we will call it the reachable postcondition of ![]() . It is just the (flattened) image
. It is just the (flattened) image ![]() of
of ![]() through
through ![]() , where the function
, where the function ![]() is defined as
is defined as ![]() .
.
The word strongest in the term strongest postcondition historically comes from Hoare logic, where one proves triples ![]() . Such a triple asserts that any output of the program
. Such a triple asserts that any output of the program ![]() resulting from an input in
resulting from an input in ![]() must be in
must be in ![]() . Formally,
. Formally, ![]() , or, equivalently,
, or, equivalently,
![]()
In Hoare logic, postconditions can be arbitrarily weakened. If ![]() and
and ![]() , then surely
, then surely ![]() . Moreover,
. Moreover, ![]() is always valid for any
is always valid for any ![]() and
and ![]() . Here,
. Here, ![]() denotes true, or the whole statespace
denotes true, or the whole statespace ![]() . Indeed,
. Indeed, ![]() always.
always.
For correctness reasoning purposes, proving ![]() with a postcondition
with a postcondition ![]() that is weaker than the strongest postcondition is OK, as long as
that is weaker than the strongest postcondition is OK, as long as ![]() describes only safe states, or good states. The strongest Hoare postcondition of
describes only safe states, or good states. The strongest Hoare postcondition of ![]() , i.e., the Hoare postcondition that provides the most information, is given by
, i.e., the Hoare postcondition that provides the most information, is given by
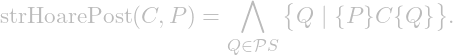
Clearly, ![]() , and if
, and if ![]() , then
, then ![]() , that is,
, that is, ![]() is indeed the strongest Hoare postcondition. Moreover,
is indeed the strongest Hoare postcondition. Moreover, ![]() That is, the strongest Hoare postcondition is equal to the reachable postcondition we are looking for—the set of all outputs reachable from
That is, the strongest Hoare postcondition is equal to the reachable postcondition we are looking for—the set of all outputs reachable from ![]() .
.
Forward Incorrectness Reasoning
The Hoare postcondition ![]() in a Hoare triple
in a Hoare triple ![]() overapproximates the postcondition (1) in Hoare logic. In O’Hearn’s recent description of incorrectness logic1, on the other hand, the reachable postcondition is underapproximated.
overapproximates the postcondition (1) in Hoare logic. In O’Hearn’s recent description of incorrectness logic1, on the other hand, the reachable postcondition is underapproximated.
An O’Hearn triple ![]() asserts that
asserts that ![]() . This is an offensive approach where we are trying to find bad states in
. This is an offensive approach where we are trying to find bad states in ![]() . If there aren’t any, then there is no guarantee of safety. But if there are, well, at least we found a bug.
. If there aren’t any, then there is no guarantee of safety. But if there are, well, at least we found a bug.
The word strongest in the traditional term strongest postcondition is no longer appropriate in the context of incorrectness logic. Indeed, in incorrectness logic, postconditions can be arbitrarily strengthened, and weaker postconditions provide more information; more possibly bad states. So let’s define the weakest O’Hearn postcondition given a precondition ![]() as
as
![Rendered by QuickLaTeX.com \begin{align*} \textup{wkOHearnPost}(C,P) = \bigvee_{Q \in \mathcal P S} \{ Q \mid [P] C [Q]\}. \end{align*}](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-f82effc2def6a0a9087937d393ac6ef6_l3.png)
Theorem. Let ![]() and
and ![]() be given. For all
be given. For all ![]() such that
such that ![]() and
and ![]() :
:
 ; and
; and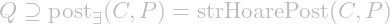 .
.
Backward Correctness Reasoning
Given a set ![]() that describes safe outputs, it can be interesting to find the set of inputs
that describes safe outputs, it can be interesting to find the set of inputs
(2) ![]()
for which all possible outputs are safe, i.e., lead to ![]() . This set is sometimes called the weakest precondition (in partially correct Hoare logic) or the weakest liberal precondition, but we will call it the safety precondition of
. This set is sometimes called the weakest precondition (in partially correct Hoare logic) or the weakest liberal precondition, but we will call it the safety precondition of ![]() . Indeed, this definition uses universal quantification to guarantee safety with the precondition; in contrast, the reachable postcondition (1) uses existential quantification (taking the image).
. Indeed, this definition uses universal quantification to guarantee safety with the precondition; in contrast, the reachable postcondition (1) uses existential quantification (taking the image).
In practice, one finds a precondition ![]() that is sufficiently safe for
that is sufficiently safe for ![]() . This means that
. This means that ![]() may exclude certain inputs that are safe to use (false negatives). This is mainly due to the possible presence of loops or (recursive) function calls.
may exclude certain inputs that are safe to use (false negatives). This is mainly due to the possible presence of loops or (recursive) function calls.
In Hoare logic, sufficiently safe means approximating the safety precondition from below. Indeed, preconditions in Hoare triples can be arbitrarily strengthened (if ![]() and
and ![]() , then surely
, then surely ![]() ), and weaker preconditions (more inputs) provide more information. Moreover,
), and weaker preconditions (more inputs) provide more information. Moreover, ![]() is always valid for any
is always valid for any ![]() and
and ![]() . Here,
. Here, ![]() denotes false, or the empty set of states.
denotes false, or the empty set of states.
Given ![]() , the weakest Hoare precondition, is defined as
, the weakest Hoare precondition, is defined as
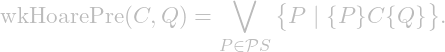
Theorem. Let ![]() and
and ![]() be given. For all
be given. For all ![]() such that
such that ![]() , we have
, we have
![]()
Backward Incorrectness Reasoning
Now using your advanced intuition for duality, looking at the theorem above about forward postcondition reasoning, we should be able to define the strongest O’Hearn precondition in incorrectness logic. Indeed, preconditions in O’Hearn reasoning can be arbitrarily weakened: if ![]() , meaning
, meaning ![]() , and we have
, and we have ![]() , then surely
, then surely ![]() . However, although
. However, although ![]() is always valid, it need not be the case that
is always valid, it need not be the case that ![]() is valid. This would namely mean that
is valid. This would namely mean that ![]() for all
for all ![]() , but this is not true: some outputs may not be reachable.
, but this is not true: some outputs may not be reachable.
The strongest O’Hearn precondition is defined as
![Rendered by QuickLaTeX.com \[\textup{strOHearnPre}(C,Q) = \bigwedge_{P \in \mathcal PS} \{ P \mid [P] C [Q] \}.\]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-d443dfe588e1d3ebfc0c40a4bb5de7da_l3.png)
The strongest O’Hearn precondition is generally speaking not comparable to the weakest Hoare precondition. In fact, it cannot be shown that ![]() if
if ![]() . Indeed, one would be obliged to show that
. Indeed, one would be obliged to show that ![]() . But taking arbitrary
. But taking arbitrary ![]() , we are not guaranteed to have an
, we are not guaranteed to have an ![]() that reaches
that reaches ![]() . Intuitively, this is because the set
. Intuitively, this is because the set ![]() uses universal quantification, whereas
uses universal quantification, whereas ![]() used existential quantification. In summary:
used existential quantification. In summary:
- In Hoare logic,
 iff
iff 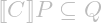 ; we can approximate the safety precondition from below and the reachable postcondition from above.
; we can approximate the safety precondition from below and the reachable postcondition from above. - In incorrectness logic,
![Rendered by QuickLaTeX.com [P] C [Q]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-6985ee57397db0697e0a54a18a79045c_l3.png) iff
iff 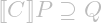 ; we can approximate the reachable postcondition from below, but we can not approximate the safety precondition from above.
; we can approximate the reachable postcondition from below, but we can not approximate the safety precondition from above.
But if you think this is the end of the story, you are in for a treat.
Backward Incorrectness Reasoning Again
The fact of the matter is that Hoare triples ![]() describe sufficiently safe preconditions
describe sufficiently safe preconditions ![]() for
for ![]() : the precondition
: the precondition ![]() may exclude certain inputs that should actually be considered safe, i.e., leading to
may exclude certain inputs that should actually be considered safe, i.e., leading to ![]() . These can be called false negatives.
. These can be called false negatives.
If, in the offensive spirit of incorrectness reasoning, we try to find a precondition for ![]() as a set of unsafe states, however, knowing that
as a set of unsafe states, however, knowing that ![]() is sufficient for
is sufficient for ![]() is not what we want. Indeed, it would be enough to know that there is an output in
is not what we want. Indeed, it would be enough to know that there is an output in ![]() reachable from
reachable from ![]() . That is, we are not chasing the safety precondition
. That is, we are not chasing the safety precondition ![]() as defined in (2), but we are chasing the reaching precondition
as defined in (2), but we are chasing the reaching precondition
(3) ![]()
that is, the preimage of ![]() . If we find this set of inputs, knowing
. If we find this set of inputs, knowing ![]() , with
, with ![]() a set of bad states, we know for sure that
a set of bad states, we know for sure that ![]() has a bad output.
has a bad output.
There is a duality between ![]() and
and ![]() , which is a direct consequence of the duality between existential and universal quantification:
, which is a direct consequence of the duality between existential and universal quantification:
(4) ![]()
As we argued above, the safety precondition ![]() can be approximated only from below. But like the reachable postcondition, the reaching precondition
can be approximated only from below. But like the reachable postcondition, the reaching precondition ![]() can also be approximated from below as well as from above, due to the existential quantification. For this, we use the following definitions:
can also be approximated from below as well as from above, due to the existential quantification. For this, we use the following definitions:
Definition (Cousot triple). A Cousot triple ![]() asserts that
asserts that ![]() , i.e.,
, i.e.,
![]()
Preconditions of Cousot triples can be arbitrarily weakened, and we have ![]() always. Define the strongest Cousot precondition as
always. Define the strongest Cousot precondition as
![Rendered by QuickLaTeX.com \[\textup{strCousotPre}(C,Q) = \bigwedge_{P\in\mathcal P S} \{ P \mid (P) C (Q) \}\]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-99f648ebeab644d130b489a8daa1a579_l3.png)
Definition (Ascari triple). An Ascari triple ![]() asserts that
asserts that ![]() , i.e.,
, i.e.,
![]()
Preconditions of Ascari triples can be arbitrarily strengthened, and we have ![]() always. Define the weakest Ascari precondition as
always. Define the weakest Ascari precondition as
![Rendered by QuickLaTeX.com \[\textup{wkAscariPre}(C,Q) = \bigvee_{P\in\mathcal P S} \{ P \mid \langle P\rangle C \langle Q\rangle \}\]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-eef0ab651803d3ef74567cfb28b2e86c_l3.png)
I named Cousot triples after Cousot & Cousot, who first described necessary preconditions2, and Ascari triples after the main author of the paper3 describing sufficient incorrectness logic.
Theorem. Let ![]() and
and ![]() be given. Let
be given. Let ![]() be such that
be such that ![]() and
and ![]() . Then
. Then
 ; and
; and .
.
To find errors, it is much more compelling to use Ascari triples (sufficient incorrectness logic). With a bad postcondition, your precondition is guaranteed to have a bad execution, which is not the case for Cousot triples, since they overapproximate. This is why Ascari et al. call their new logic sufficient incorrectness logic: the preconditions you find are sufficiently incorrect.
There is the following neat correspondence between Cousot triples and Hoare triples, which resembles the duality in the Lemma (4) above between the reaching precondition and safety precondition:
Theorem. For all predicates ![]() :
: ![]() if and only if
if and only if ![]() .
.
I only show ![]() . The goal is to show that
. The goal is to show that ![]() , or, equivalently, that
, or, equivalently, that ![]() . Let
. Let ![]() and suppose also
and suppose also ![]() . Then there is
. Then there is ![]() such that
such that ![]() . This contradicts
. This contradicts ![]() .
. □
It is tempting to conjecture that also ![]() if and only if
if and only if ![]() . This is not true in general however, due to existential quantification. Indeed, suppose
. This is not true in general however, due to existential quantification. Indeed, suppose ![]() , i.e.,
, i.e., ![]() . In this situation, it is still possible that there is an
. In this situation, it is still possible that there is an ![]() in
in ![]() reachable from some
reachable from some ![]() not in
not in ![]() that does not reach into
that does not reach into ![]() . That is, nothing about this guarantees
. That is, nothing about this guarantees ![]() . The following picture should make this clear:
. The following picture should make this clear:
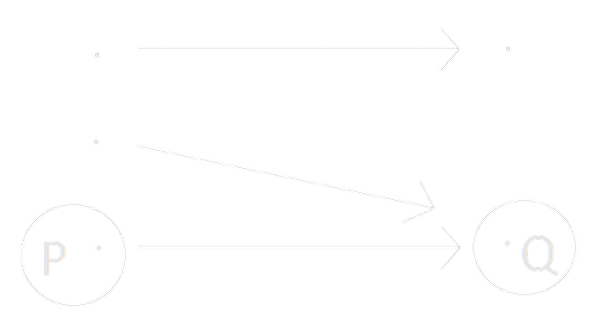
In this situation, we have ![]() , but not
, but not ![]() .
.
Postconditions Again
For the sake of completeness, we should define the postcondition dual to the reachable postcondition:
![]()
Frankly, I have no idea why this set could be interesting in the least. Clearly, by duality of existential and universal quantifier, we have the following:
Lemma. Let ![]() be a predicate. Then
be a predicate. Then ![]() .
.
Postconditions in Cousot triples can be arbitrarily strengthened, and we always have ![]() . Postconditions in Ascari triples can always be weakened, but we do not necessarily always have
. Postconditions in Ascari triples can always be weakened, but we do not necessarily always have ![]() , because we do not know if all outputs are reachable.
, because we do not know if all outputs are reachable.
We can approximate the dual postcondition from below using Cousot triples, by defining
![Rendered by QuickLaTeX.com \[\textup{wkCousotPost}(C,P) = \bigvee_{Q \in \mathcal P S} \{ Q \mid (P) C (Q) \}\]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-e08b0ae5d56b82ecfe0953284c5f13a8_l3.png)
We then have:
Theorem. Let ![]() and
and ![]() be given. Let
be given. Let ![]() be such that
be such that ![]() . Then
. Then
![]()
We can attempt to approximate the dual postcondition from above by using Ascari triples, by defining
![Rendered by QuickLaTeX.com \[\textup{strAscariPost}(C,P) = \bigwedge_{Q \in \mathcal P S} \{ Q \mid \langle P \rangle C \langle Q \rangle \}\]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-1cf759c2fcdd10cf68e9d3f47c511d69_l3.png)
Like with the safety precondition, however, this fails again due to universal quantification.
In summary:
- In Hoare logic,
 iff
iff 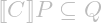 ; we can approximate the sufficient precondition from below and the reachable postcondition from above.
; we can approximate the sufficient precondition from below and the reachable postcondition from above. - In incorrectness logic,
![Rendered by QuickLaTeX.com [P] C [Q]](https://erikvoogd.nl/wp-content/ql-cache/quicklatex.com-6985ee57397db0697e0a54a18a79045c_l3.png) iff
iff 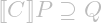 ; we can approximate the reachable postcondition from below, but we can not approximate the sufficient precondition from above.
; we can approximate the reachable postcondition from below, but we can not approximate the sufficient precondition from above. - With necessary condition triples,
 iff
iff  ; we can approximate the reaching precondition from above and the dual postcondition from below.
; we can approximate the reaching precondition from above and the dual postcondition from below. - With sufficient incorrectness triples,
 iff
iff  ; we can approximate the reaching precondition from below, but we can not approximate the dual postcondition from above.
; we can approximate the reaching precondition from below, but we can not approximate the dual postcondition from above.
- O’Hearn, P. W. (2019). Incorrectness logic. Proceedings of the ACM on Programming Languages, 4(POPL), 1-32.
- Cousot, P., Cousot, R., Fähndrich, M., & Logozzo, F. (2013, January). Automatic inference of necessary preconditions. In International Workshop on Verification, Model Checking, and Abstract Interpretation (pp. 128-148). Berlin, Heidelberg: Springer Berlin Heidelberg.
- Ascari, F., Bruni, R., Gori, R., & Logozzo, F. (2023). Sufficient Incorrectness Logic: SIL and Separation SIL. arXiv preprint arXiv:2310.18156.

Leave a reply!